Seeing with"Gaussian" Kernels: How Distance Becomes Meaning

Vija Celmins – Night Sky #19 (1998)

“The stars are not connected, but our mind connects them — just as kernels give meaning to nearby points.” - by dayun.H

How I first met Kernels...

I first met the word kernel by accident... It was Thursday, March 20th — the day of the General Chemistry II prelim. I was working as a lab TA and had to proctor the exam. While preparing the room, I noticed a sheet left behind — probably from a CS 3xxx class. The first page was covered in matrix notation, and right at the top: “kernel function.” I didn’t know what it meant, and I cannot believe myself there are still so huge world that I haven't met yet.. It stuck on me and kept echoing in my head. I’d already been curious about machine learning, quantum computing, and logic gates, so that single word became the starting point. I went home and began to study. That’s how I met the kernel.....

My ta session.. not as student.. ta mode..

Start! Gaussian Kernel

The Gaussian kernel model is fundamentally about finding the output of a new input based on its distance relationship to the existing training points. But the phrase "finding distance relationship" contains much deeper meaning than it first appears.

While the model begins with a 2D map, it's important to remember that this 2D space often comes from dimensionality reduction. In reality, the data may contain many properties. For example, if we’re classifying cats and dogs, the data could include features like fur color, body size, ear shape, etc. If we consider just three features, then each animal would exist in a 3D feature space.

However, we often reduce that higher-dimensional space to 2D using techniques like PCA or t-SNE for visualization or efficient learning. That means the data we're working with in kernel models — although appearing 2D — actually encodes compressed information from many physical or descriptive properties .

That’s where the kernel trick comes in. Since so much information is compressed into a lower-dimensional map, we can’t easily distinguish complex subcategories like Persian cat vs. Ragdoll vs. Golden Retriever vs. Maltese, just by drawing a simple boundary. We need a way to expand the representation back to something more expressive — and that’s exactly what a kernel function like the Gaussian kernel does.

I chose to focus on the Gaussian kernel first, because the term reminds me of Gaussian functions in chemistry, especially in quantum chemistry where they are used to approximate atomic orbitals. Because of mainly two conditions we choose gaussian function as basic of orbitals. First is that it is the function that matches with a minimum limit of the Heisenberg uncertainty principle. Which is delta x * delta p = h bar /2. Which is maximum localized function without violating quantum basis principle. The second is that it is the one that satisfies the harmonic oscillator equation. Anyway for these reasons, everyday I encounter word “gaussian”. And here I met “Gaussian” again for one of the kernel method which was destiny to me.  

To start, input x = |x-x'| where x and x' are both inputs.

If there are four inputs, then (1,2) (1,3) ... becomes distance. If there is zero distance, which means the same input (1,1), (2,2),..., then the Gaussian gives out 1. That Gaussian result is noted as a K value, how similar it is between the two inputs.

It makes sense because the distance encompasses not only 2D distance but also overall property distances. So, property distances show how similar they are, and large numbers indicate that they are very similar. Thus, a row-column 1234 input makes a 4x4 matrix here. this is a gram matrix.

Overall simple scheme

Our purpose here is to make a linear relationship between real output "cat or dog" but not limited to these. We can expand "cat, dog, dolphin, etc.."

However, because the input is not linear, we are trying our best to modulate by shifting K by a lambda amount and creating a linear slope sigma.

Lambda reflects how much we will consider the actual data of K. When lambda is small, we will reflect the raw data more. Alpha in here is (4*1).

Since K has labeled 1234 input in both rows and columns, alpha reflects all the input indices, even if it seems to be calculated based only on the distance scale.

That was the point I was initially slightly confused.

Composite function - making linearity

Once alpha and lambda are obtained, we can now put new input x*.

This started to calculate the distance between the original training model with x1, x2, x3, x4, and 4 inputs and then put it into the Gaussian function to calculate similarity and then weighted with corresponding input alpha.

It seems to me it was just a linear combination of orbitals which is the hybridization of orbitals, mainly well-known as sp3; each orbital also has a weighted coefficient. Actually, this Gaussian kernel function calculation seems to me just the same process of composite function calculation because input makes  f1(x) = |x-x1|= t, f2(t) = p = Gaussian function, f3(p) = alpha*p = f3(f2(f1(t))).

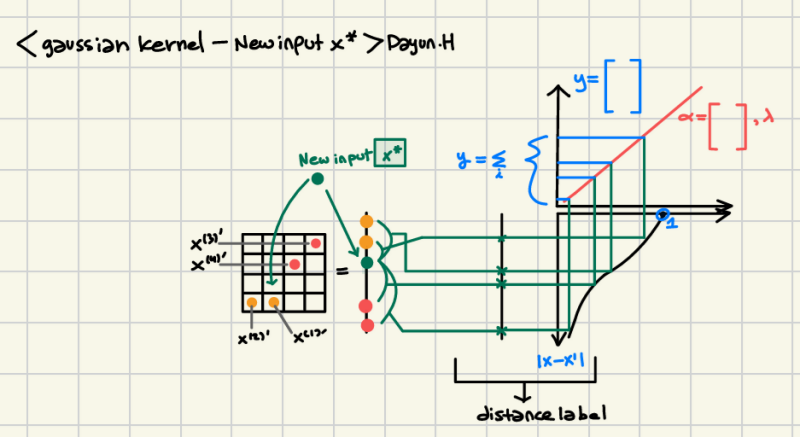
New input based on already made alpha matrix